
三平方の定理と平面図形 現役塾講師のわかりやすい中学数学の解き方
図形・三平方の定理 入試最頻出の三平方の定理です。 別名「ピタゴラスの定理」とも呼ばれ、数学におけるもっとも有名な定理の1つでしょう。 入試においては、単独での出題ではなく、他の分野との融合がよく見られます。 基礎的なことは、やはり 算数・数学の命題・公理・公準・定義・定理・系・性質・公式・原理・法則の違い 数学はまさにピラミッド 数学っていうのは,正しいことだけを積み重ねたまさにピラミッドのようなもの。 昔から多くの数学者が取り組んでいて、いくつかのピラミッド
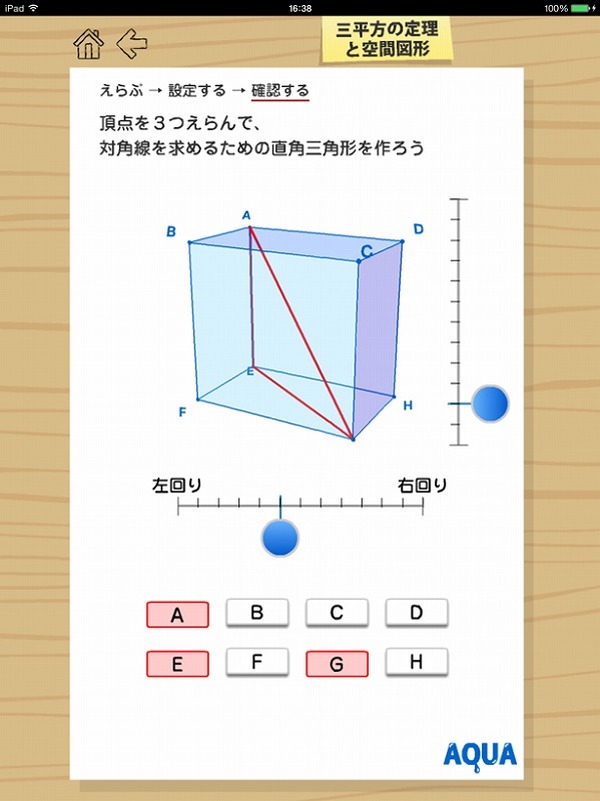
中学数学 三平方の定理 空間図形
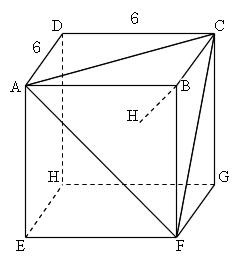
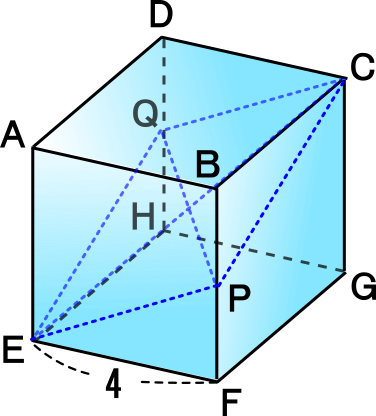
中学数学 三平方の定理 空間図形-解答下の図の水色の直角三角形に三平方の定理を用います。 \(OH\) の長さを \(xcm\) とすると\(x^24^2=10^2\)\(x^216=100\)\(x^2=100 中学数学の基本から難問までの問題と分かりやすい解説を掲載した完全無料のオンライン学習ページです。数学・算数 中学生(三平方の定理と空間図形) A,B,C,D,E,F,G,Hを頂点とする立方体がある。この立方体の対角線AGの長さが6cm

三平方の定理を使って線分の長さを求める問題の解き方 現役塾講師のわかりやすい中学数学の解き方
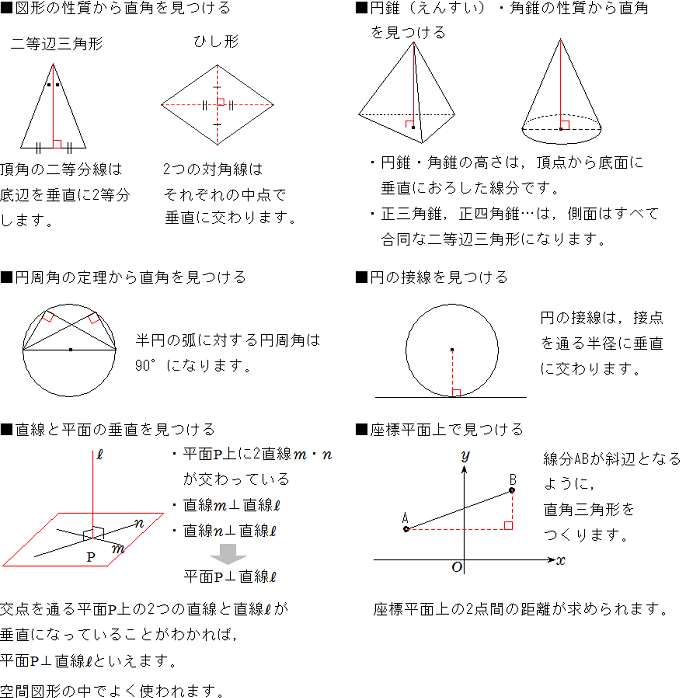
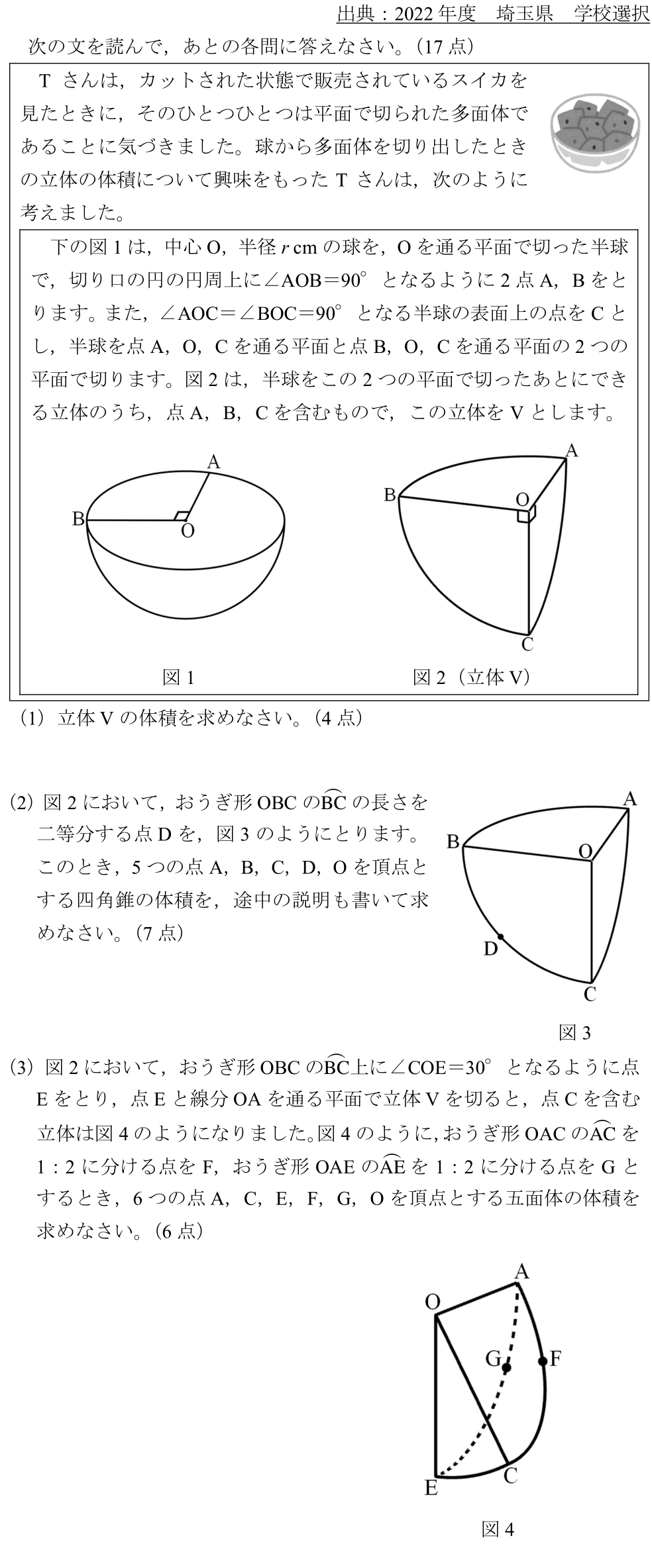
三平方の定理を用いた問題 最も基本的な問題は、直角三角形の辺の長さを求める問題でしょう。 それは、平面図形に限らず、空間図形(立体図形)においても使えるので、問題をしてよく使われています。 複雑な図形では、どこに直角三角形が隠れているのかを見つけることが必要となってきますので、色々なケースを経験して身に付けていきましょう。 直角三角形の一辺の長さを求める 最も基本中学入試の素養必要かもしれません。 ・そんなのアリ空間図形(★★★★★)(22年度埼玉県学校選択) よくある典型問題かと思いきや,そうじゃない捻った問題です。 ・正答率00%スクリーンと回転空間図形(★★★★★)(21年度宮崎県) 45°の使い方。 中学数学3分でわかる!相対度数の求め方 中2数学 150 2直線の交点の座標の求め方がわかる3ステップ 中1数学 23 円柱を2つ重ねた立体の表面積の求め方 中2数学 1000%忘れない!合同の記号(≡)の2つの覚え方 中3数学
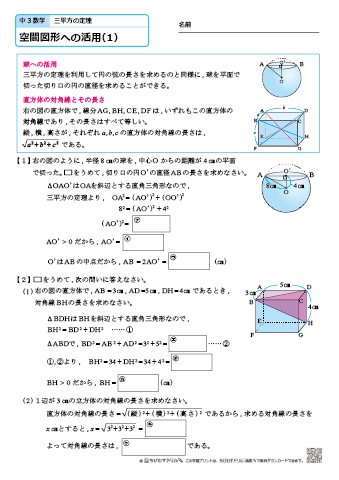
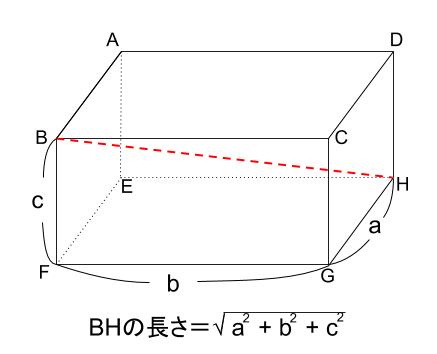
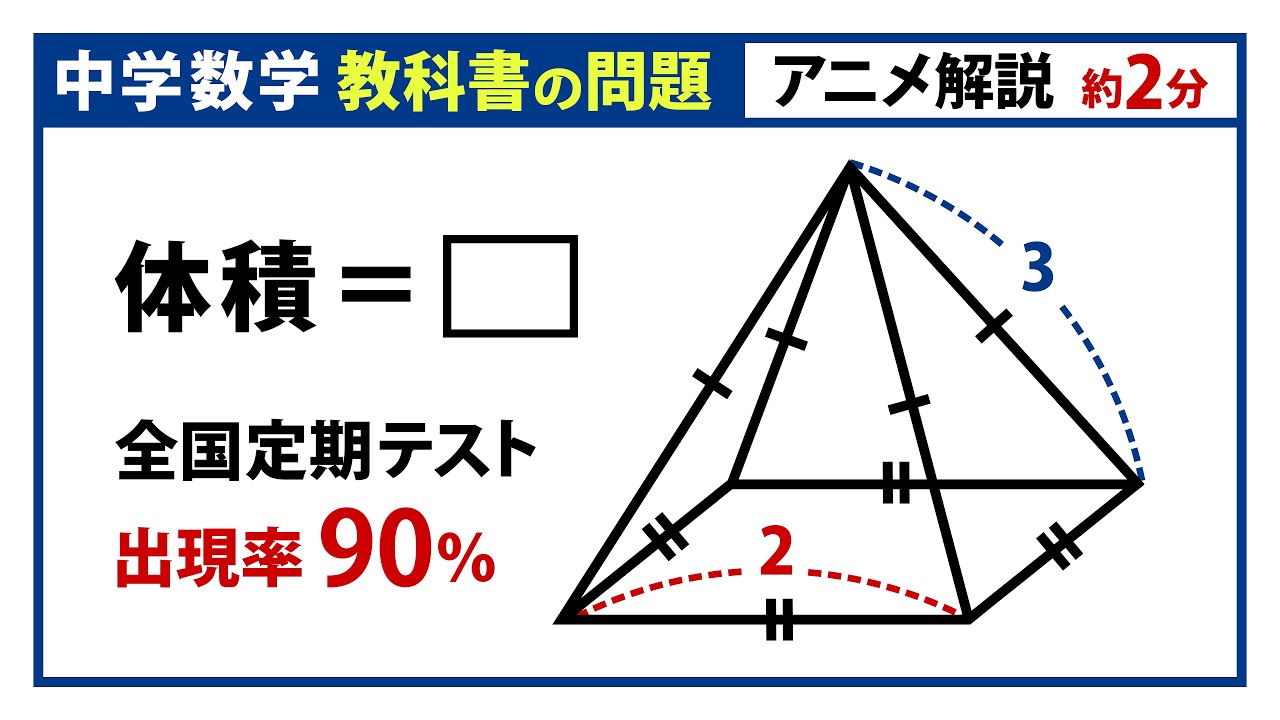
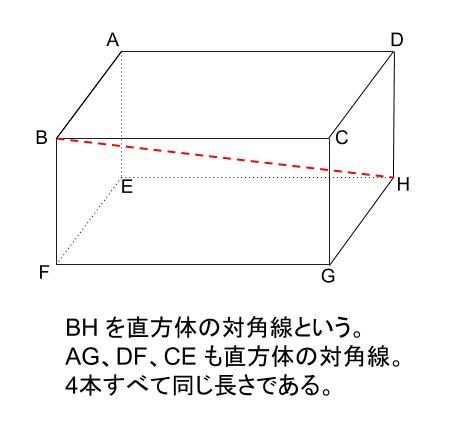
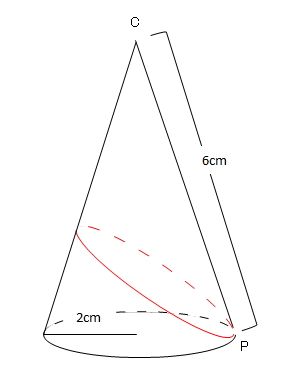
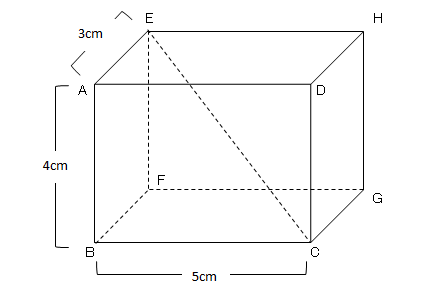
相似*円周角*三平方の定理などの高校で習う公式 (中3が使いやすいように改良笑)や自己流に編み出した公式集 ( ´ ` )ノ 自分用に作ったので見やすさは重視してません (=゚ω゚)ノ 数学 暗記 裏技 公式 円周角 三平方の定理 面積求め方 円錐 相似な図形空間図形への利用 目次 直方体の対角線 公式 円錐の体積 角錐の体積 四角錐の体積 正四面体の体積 他の要点、例題・練習問題 三平方の定理が使えるのは直角三角形である。 定理を利用する場合は図から直角三角形を探すか、補助線を書いて直角三角形を作る。 立体は切断したり、展開したりしてできる限り平面で考える 直方体の対角線 例 対角線の長さBHを求める。 A B C D E F G H 5cm 4cm円錐の体積の求め方を確認しておくと こうでしたね。 コレに当てはめて考えていきましょう。 底面積は円の面積公式 に当てはめて となるので、体積は となりました。 三平方の定理を使って 高さを求めることができれば あとは1年生で学習したこと
中学数学 三平方の定理 空間図形のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
「中学数学 三平方の定理 空間図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「中学数学 三平方の定理 空間図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「中学数学 三平方の定理 空間図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「中学数学 三平方の定理 空間図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「中学数学 三平方の定理 空間図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
「中学数学 三平方の定理 空間図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「中学数学 三平方の定理 空間図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「中学数学 三平方の定理 空間図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
「中学数学 三平方の定理 空間図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「中学数学 三平方の定理 空間図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「中学数学 三平方の定理 空間図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
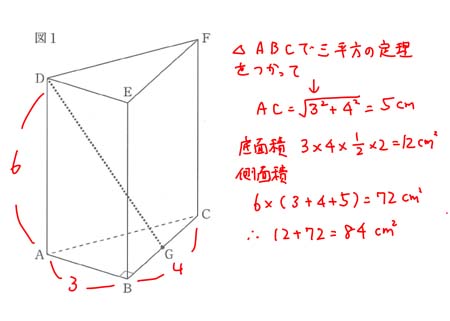
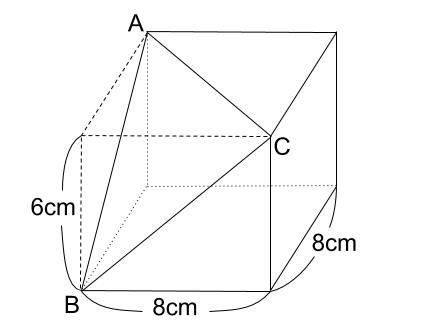
これより三平方の定理を用いて、 A C ² = 4 ² 10 ² A C ² = 4 ² 10 ² A C ² = 116 A C ² = 116 A C = 2 √ 29 A C = 2 29 さらに問題です。 1 1 辺 8cm 8 c m の立方体の頂点や返上の点を結んでできる次の図形(影の部分)の面積を求めなさい。 ただし、点 S S は AE A E の三平方の定理(ピタゴラスの定理)は中学3年間のまとめ分野になります。 教科書に出てくる定理は1つだけで覚えるのも簡単です。 長さを求める定理なので、面積、体積を求める問題に使うことが多くなります。 三平方の定理が直接問題
Incoming Term: 中学数学 三平方の定理 空間図形,




0 件のコメント:
コメントを投稿